Calendrier Juif – L’origine de la connaissance du cycle lunaire

Ce mois-ci sera pour vous le premier des mois

(chémot 12, 2)

Le calendrier Hébraïque, sur lequel nous nous basons jusqu’à aujourd’hui pour fixer les dates de fêtes juives, a été institué, selon une tradition rapportée par Rav Haï Gaon (XIe siècle, cité par Avraham bar Hiyya dans son Sefer Ha’ibbour, rédigé en 1123), par Hillel Néssia (ou Hillel II) en l’an 359 de l’ère courante. Hillel établit les règles de calculs afin de mettre en place un calendrier perpétuel. Les règles qu’il rend publiques sont encore celles observées aujourd’hui.

Avant cela, il n’y avait pas de règles préétablies pour fixer les dates du calendrier, mais elles étaient fixées sur la base d’observations astronomiques, météorologique et même agricoles. La première visibilité du croissant de la nouvelle lune après une conjonction lunaire (appelé Molad – naissance), permettait de fixer la néoménie. La décision de fixer une année comme Méouberet (embolismique) ou non, dépendait de facteurs agricoles ainsi que de la Tékoufa (saison astronomique). Ces décisions étaient sous l’entière responsabilité du Sanhedrin, la plus grande autorité rabbinique, établi en terre d’Israël. C’est ainsi que le peuple d’Israël pratiquait depuis sa création, pendant près de 1700 ans.

Ce n’est qu’après la conquête de Jérusalem par l’empire romain, et tandis que l’existence même du Sanhédrin était menacée, et que les cérémonies d’annonces de la nouvelle lune furent interdites par l’empereur romain Constance II, que fut établi le calendrier de Hillel, qui permet ainsi au judaïsme de se perpétuer indépendamment de l’avenir de cette institution.

Les données astronomiques à partir desquels il fonde son calendrier sont principalement:

• Le mois lunaire qui correspond à la révolution synodique, et dure 29 jours, 12 heures et 793 ‘halaquim (parts) (1 ‘heleq = 3.33 secondes, puisque 1 heure = 1080 ‘halaquim).
• L’année solaire, basé sur la tradition transmise par Rav Ada qui évalue sa durée à 365 jours 5 heures et 997 ‘halaquim, soit 365.2468 jours (contre 365.2425 jours pour l’année grégorienne, une différence d’environ 1 jour tous les 230 ans).
• le rapport cyclique de 19 ans entre les mois lunaires et les années solaires, connu sous le nom de cycle métonnique (décrit par Méton d’Athène il y a presque 2500 ans), où l’on place des années embolismiques (de 13 mois) aux rangs 3, 6, 8, 11, 14, 17 et 19 du cycle, pour faire correspondre l’année lunaire à l’année solaire (19 ans = 235 mois).

Ces données ont fait leurs preuves et se sont avérées très précises, vérifiées déjà par le calendrier qui est resté en phase avec à la réalité des saisons jusque aujourd’hui. En effet, cette mesure de temps du cycle lunaire, considéré par Hillel à 29j 12h 793p, correspond précisément à la durée moyenne d’un mois synodique prouvée par la science que récemment, à l’aide de moyens électroniques perfectionnés, à savoir : 29.530588 jours. Car si on convertit 12h + 793p en nombre décimal (par rapport à 1 jour), alors on obtiendra 1/2j + 793/25920j = 0.5j + 0.03059j = 0.53059. On aura en conclusion une lunaison à 29.53059j, chiffre identique à celui obtenu par la science il y a quelques années. En 1984, le chef de l’institut spatial américain (N.A.S.A.) Carl Sagan déduit de sa recherche que la durée de renouvellement de la lune est de 29.530588 jours.

On peut alors s’interroger sur l’origine de ces connaissances. Quelle est la véritable source de ces données astronomiques sur lequel a été construit notre calendrier ? Est-il plausible de dire que les détails scientifiques du calendrier avaient déjà été enseignés à Moshé au Sinaï, alors qu’ils n’avaient aucune implication Halakhique pour les siècles qui ont suivi, et n’eurent de nécessité que 1700 ans plus tard ?

La transmission de Raban Gamliel et les sources babyloniennes

Dans le Talmud (roch hachana 25a), nos maîtres nous enseignent qu’il arriva une fois, une brume apparut dans le ciel et l’on crut voir la nouvelle lune. Alors que le peuple allait proclamer Roch ‘Hodech, Raban Gamliel n’a pas hésité à contester leur avis et proclama: « Dans la maison de mon grand père, on tenait comme principe que la lune se renouvelait au minimum tous les 29 jours et demi, 2/3 d’heure et 73 parts ». Ces paroles de Raban Gamliel nous laisseraient entendre à priori que cet indice se transmettait déjà dans la tradition orale.

Pourtant, cette durée du mois lunaire 29, 12, 793, décrite dans le Talmud et sur laquelle est fondé notre calendrier, apparait en fait plusieurs centaines d’années auparavant dans les écrits babyloniens, puis par les Grecs dans le livre d’astronomie grec le plus célèbre – l’Almageste, datant du II ^e siècle, et écrit par Talmay, plus connu sous le nom de Ptolémée (ou Ptolemaeus).

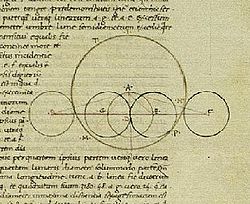
Dans ce livre, on trouve décrit l’intervalle de temps séparant deux nouvelles lunes, qui est formulé comme ceci: 29, 31′ 50” 8”’ 20””. Cette valeur se déchiffre  à partir du système de numération à base 60, appelé sexagésimal (Par exemple: 75 en base 10 s’écrit 1,15′ en base 60), beaucoup utilisé par les astronomes et géographes grecs tels que Ptolémée ou Théon d’Alexandrie. On comprendra leur description ainsi: 29 jours + 31/60 + 50/3600 + 8/216000 + 20/12960000). Dans ce livre, est présentée également la manière dont Hipparque avait déjà calculé cela, 300 ans avant Ptolémée. Il convient de souligner que cette méthode a été poursuivie par les astronomes musulmans au Moyen-Âge et a donné des résultats divers, un peu plus brefs.

En conclusion, les sages juifs avaient certes une connaissance très précise des valeurs astronomiques de la lune, absolument incroyable pour l’époque. Toutefois, il est difficile de s’appuyer là-dessus pour prouver la véracité de la Torah, puisque les Babyloniens détenaient déjà une connaissance ultra précise de la révolution lunaire plus d’un millénaire avant la rédaction du Talmud, se basant sur l’observation des éclipses.

Il est vrai que l’on trouve un certain nombre de connaissances qui, sans être explicite dans la Torah écrite, étaient pourtant transmises de génération en génération jusqu’à Moshé Rabeinou. Toutefois, concernant la révolution de la lune autour de la terre, même si tout porte à croire que les juifs disposaient de cette information depuis l’époque de Moshé, cela n’est pas explicite dans le Talmud même, et aucune indication ne nous est donnée clairement à ce sujet.

Qu’en disent nos sources anciennes ?

La plupart des anciens commentateurs qui ont traité de ce domaine ont affirmé que l’origine de cette connaissance était due à une recherche scientifique et non comme une transmission depuis Sinaï. Il est raconté dans un Midrach rapporté dans le Smak (mitsva 103) comme quoi les enfants d’Issachar sont arrivés à définir la durée du mois lunaire à l’aide de différents tests et expérimentations. On trouve cette approche dans le livre Evronot de rav Eliezer Bellin (17^e siecle), le livre Itim Lébinah (§1) de rav Yossef Ginzbourg, ou encore Tehounat Chamaym (§53) de rav Rephael Hanover, et beaucoup d’autres, qui considèrent tous que seule la recherche scientifique à l’aide de l’expérience et de l’observation peuvent être à l’origine de ce savoir.

Certains ont même écrit que les Sages l’avaient reçue des savants d’autres nations. C’est entre autre l’opinion de Haïm Slonimsky  dans son livre Yessodé Haibour (3, 46).

Néanmoins, on trouve certains avis parmi les Richonim et Aharonim, qui estiment l’origine de cette instruction qui apparait dans la Guémara comme étant soit transmise depuis le Sinaï soit d’origine prophétique. La plupart d’entre eux n’ont pas eu besoin de preuve à l’appui, comme on peut lire dans les écrits de Rav David Gans (Prague, contemporain de Galilée au XVIe siècle) dans son livre Nehmad Vénai’m (§213) : « c’est un compte très profond et merveilleux, plus précis que tous les comptes des astronomes anciens et récents… Et les sages des nations nous ont déjà remerciés pour cela… Qui nous a dévoilé ce compte tellement précis?…la tradition transmise par nos ancêtres remontant jusqu’au au mont Sinaï ».

Sont de cet avis également rav Yehuda Halevi (XII siècle) dans son Kuzari (4, 29), ainsi que rav Itshak Haisraéli (disciple du Roch, XIV siècle) dans son livre Yesod O’lam (3,12) qui eux, ont trouvé la nécessité de démontrer cette opinion. Leur avis repose principalement sur le fait que bien qu’il n’y ait pas de source religieuse certifiant qu’il s’agit d’une donnée transmise à Moché ou d’une autre forme de prophétie, malgré tout, cela ne peut être interprété autrement dans la mesure où il n’y avait aucun moyen naturel de calculer cela avec une telle précision, et donc il s’agit forcément d’une connaissance spirituelle.

Il nous est difficile de comprendre comment le Kuzari et le Yesod O’lam qui vivaient en Espagne, où la connaissance des sciences ainsi que les livres de savants grecs étaient très répandues, ont ils pu affirmer que les nations ne pouvaient arriver à de telles précisions. La question s’accentue davantage concernant le Yesod O’lam qui traite entièrement de l’astronomie selon les concepts grecs, et en plus de cela il rapporte au nom de l’Almageste la durée du cycle lunaire et les moyens de calculs pour la déduire.

De plus, La simple affirmation que notre mois lunaire est sans aucune approximation est inexacte. La valeur que nous connaissons aujourd’hui est inférieure à cette valeur de près d’une demi-seconde. À l’époque des ancêtres de Raban Gamliel, l’écart était probablement plus faible, mais n’était toujours pas exact. Même des écrits de Maïmonide, qui connaissait la science grecque et musulmane (citée parfois dans son livre Michné Torah – voir Kidouch ha’hodech 17, 24), il ressort que bien que notre calendrier se base sur cette valeur de 29,12,793, néanmoins il existe une valeur plus précise, légèrement plus courte.

Problématique sur le livre Yesod O’lam

On trouve une autre difficulté dans le livre Yesod O’lam, où rav Itshak Haisraéli apporte au nom de l’Almageste la durée moyenne du mois lunaire, qu’il formule d’après le système de numération à base 60 comme ceci: 29 jours 31′ 50” 8”’ 9”” 20””’. Est-ce vraiment la valeur écrite dans l’Almageste? Une simple vérification nous montrera qu’il y a là une erreur de retranscription, le chiffre 9 entre le 8 et le 20 est un rajout du Yessod O’lam, de tel sorte que la valeur est diminuée (de 1/14 de seconde).

Et d’ailleurs dans ce même livre, est écrit juste après cela que cette valeur prise en considération par les Grecs était légèrement inférieure à celle connue par nos sages. Si c’est le cas, on comprend comment il a conclu que les savants des nations ne pouvaient pas atteindre l’exactitude des sages. Il reste à comprendre, quelle est la source de cette erreur fondamentale?

Si nous consultons le livre d’Almageste dans les versions qui existaient au Moyen Âge, la réponse sera très simple. À cette époque, dans les traductions en latin, arabe et hébreu, il y avait une légère erreur dans la copie de cette valeur. En effet, le chiffre 9 leur a été ajouté comme la retranscrit le Yessod O’lam. Mais dans l’origine grecque, dans divers exemplaires, ce chiffre n’apparait pas mais est expressément énoncé: 29 31′ 50” 8”’ 20”’ (κθ, λα, ν, η, κ).

L’explication courante de cet écart est rattachée aux calculs d’Hipparque qui se base sur l’intervalle de deux éclipses lunaire espacés de 126007 jour et une heure, soit 4267 mois, et le résultat de ce calcul donnant effectivement la valeur de 29,31,50,8,9,20. Mais en fait, Hipparque connaissait la valeur de 29,31,50,8,20 qui était entre les mains des Babyloniens et étant donné que la différence entre cette valeur et son calcul est négligeable, il l’a arrondie et a laissé la valeur des Babyloniens.